GNN 공부를 위한 내용 정리입니다.
CS224W Winter 22/23 자료를 기준으로 내용을 정리했습니다.
연구실에서 GNN을 많이 활용하는만큼 GNN을 조금 더 자세하게 이해하고 있는게 좋을 것 같다고 생각하게 되었습니다.
그래서 CS224W를 기반으로 GNN과 관련된 내용을 정리해보고자 합니다.

그래프는 관계를 가지는 무언가를 표현하는 일반적인 방법입니다.



세상에는 위와 같이 그래프로 표현될 수 있는 수많은 데이터가 존재합니다.

이처럼 복잡한 도메인은 풍부한 관계 구조를 가지고 있으며 이는 그래프로 표현될 수 있습니다.
그래프를 활용하여 관계를 명시적으로 모델링함으로서 더 좋은 성능을 달성할 수 있습니다.
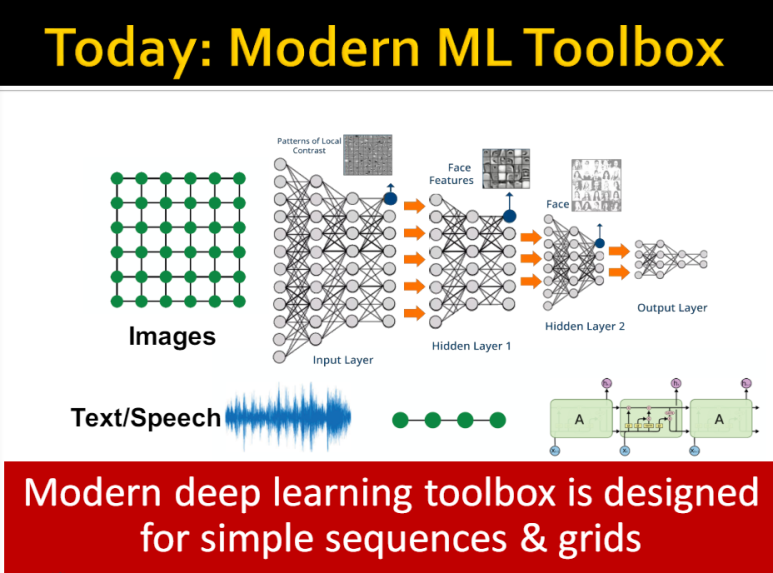
오늘날 많은 딥러닝 모델이 간단한 시퀀스(ex. Text, Time Series,Voice) 혹은 그리드(ex. Image) 형태의 데이터를 위해 설계되었습니다.

그러나 모든 것이 시퀀소 혹은 그리드 형태로 표현될 수는 없습니다.
그래프의 경우가 그렇습니다.

그래프 데이터를 활용한 딥러닝 모델을 만들고 싶어도 이는 아주 어렵습니다.
데이터마다 사이즈가 다르고(arbitrary size), 데이터의 구조가 복잡하기(complex topological structure) 때문입니다.
또한 그리드(ex. Image)와 같은 공간적 지역성(spatial locality)이 없기 때문에 고정된 노드의 순서 혹은 기준점이 없어 어려운 것입니다.
즉, 그리드 혹은 시퀀스와 같은 데이터는 고정된 형태가 있어 다루기 쉽지만, Graph는 고정된 형태가 없기 때문에 다루기가 어렵습니다.
이를 해결하기 위해 GNN에 대한 연구가 진행되고 있습니다.

크게 보면 그래프를 위한 모델링에서 입력 데이터(Input data)는 그래프 전체 구조(Network, Graph 는 같은 의미)를 활용합니다.
이를 Graph convolutions(GNN Layer)를 통과시킨 후 일반적인 딥러닝 모델과 같이 활성화 함수, 정규화 등의 과정을 거쳐 최종적으로 필요한 Task를 수행합니다.

GNN은 각 노드들이 딥러닝을 활용하여 이웃들의 정보를 모을 수 있도록(aggregate) 돕습니다.
즉, 그래프 데이터에서 각 노드는 자신의 특성만을 갖고 있는 것이 아니라 연결된 이웃 노드들의 특성도 반영해야 그래프를 다루는 의미가 있습니다.
예를 들어, SNS에서 한 사람이 인플루언서인지 보기 위해서는 그 사람의 팔로워 혹은 팔로잉을 고려하는 것이 인플루언서인지 판단하기 유리해집니다.

따라서 GNN의 핵심 아이디어는 바로 모든 노드를 그들의 이웃 정보를 활용하여 계산 그래프(computation graph)로 정의하는 것입니다.

GNN은 노드들이 그들의 이웃 정보를 모을 수 있도록 돕는 특성이 있어 과거의 ML(머신러닝) Task에서 Feature Engineering 부분을 하지 않아도 괜찮다는 장점이 있습니다.
표현을 학습(representation learning)하기 때문에 자동으로 feature를 학습하는 것입니다.
여기서 representation learning이란 어떤 Task를 수행하기 위해 데이터의 표현(representation)을 변형하는 방법을 학습하는 것입니다.
한 번 더 풀어서 설명해 보면 Raw data를 별도의 처리 없이 모델에 넣어 데이터의 구조를 학습하여 데이터를 잘 나타낼 수 있는 최적의 표현(representation)을 결정하고, 이를 토대로 우리는 원하는 Task를 수행할 수 있게 되는 것입니다.

앞서 설명한 것처럼 GNN으로 Graph의 representation을 학습하는데, 이는 각각의 노드를 d 차원으로 임베딩함으로서 가능해집니다.
GNN을 통해 만든 d 차원의 표현이 좋으면 수행하고자 하는 Task에 적용이 잘 되어 좋은 성능을 보일 것입니다.
그렇기에 Graph를 d 차원으로 임베딩 할 때 표현력이 풍부해지도록 잘 임베딩하는 것이 목표입니다.

CS224W에서는 그래프를 위한 기계학습을 공부하기 위해 전통적인 방법인 Graphlet, Graph Kernel과 노드 임베딩 방법인 DeepWalk, Node2Vec, GNN 모델인 GCN, GraphSAGE, GAT 등에 대해 학습합니다.

GNN은 전체 그래프를 활용하는 Graph level task부터 부분적인 그래프를 사용하는 Subgraph level task, 노드 간의 연결(Edge or Link)에 대한 Edge level task, 노드에 대한 Node level task 등을 수행할 수 있습니다.

또한 Graph의 기계학습 종류는 Node Classification, Link Prediction 등이 있습니다.
GNN에서 특히 Node Classification, Link Prediction, Graph Classification Task를 많이 다룹니다.
(Example 부분은 넘어가도록 하겠습니다.)

그래프의 구성요소는 위와 같습니다.

왼쪽 위의 배우들의 관계도를 예시로 살펴보면 node or vertice는 각 배우(Actor 1, Actor2, ...)가 되고, link or edge는 영화(Movie 1, Movie 2, ...)가 됩니다.
그리고 System은 모든 node와 edge를 포함하는 network or graph가 됩니다.

여기서부터는 그래프에 대해 조금 더 자세하게 다룹니다.
먼저 그래프 데이터는 크게 방향이 없는 그래프 데이터(Undirected)와 방향이 존재하는 그래프 데이터(Directed)로 나눌 수 있습니다.
방향이 없다는 것은 연결이 양방향이라고 볼 수 있습니다.

그래프 데이터는 사실 상상도 못할 정도로 복잡한 경우도 있습니다.
따라서 더 다양한 것을 고려하기 위해 노드와 엣지의 타입이 여러 가지인 Heterogeneous graph도 있습니다.
(여기서는 이런 그래프도 있다 정도로 알고 넘어가면 될 것 같습니다.)

세상의 많은 그래프 데이터는 사실 Heterogeneous graph입니다.
(위와 같이 이런 그래프가 Heterogeneous graph이구나 정도로 생각하고 넘어가면 될 것 같습니다.)

그래프 데이터는 Node Degree를 가집니다.
Node Degree는 어떤 특정 노드에 연결된 Edge의 수를 의미하며 이는 Undirected인 경우와 Directed인 경우 다른 Node Degree를 가집니다.
1). Undirected

먼저, Undirected의 경우 단순하게 특정 노드에 연결된 Edge의 수를 의미합니다.
위의 그림을 예시로 살펴보면 노드 A의 Node Degree는 연결된 Edge의 수인 4가 됩니다.
이를 표현하면 다음과 같습니다. $k_A = 4$
또한 모든 노드에 대해 Node Degree의 평균값을 구할 수 있으며, 수식은 아래와 같습니다.
$$ \overline{k}=\frac{1}{N}\sum_{i=1}^{N}k_i=\frac{2E}{N}$$
수식을 좀 더 살펴보면, N 은 전체 노드의 수를 의미하며, k_i 는 i번째 노드의 Node Degree를 의미합니다.
또한, 하나의 Edge에 2번 계산되기 때문에 2E 로 계산합니다.
아래의 그림으로 조금 더 살펴보겠습니다.(굿노트에 직접 그려서 좀 못 생겼습니다..)

위와 같은 그래프가 있을 때 노드 A에 대한 Node Degree를 계산할 때 C와 E가 연결되어 있기 때문에 2가 됩니다.
노드 C에 대한 Node Degree를 계산할 때 A, B, E가 연결되어 있기 때문에 3이 됩니다.
그런데 노드 A의 Node Degree를 구할 때와 노드 C의 Node Degree를 구할 때 동그라미 친 부분은 2번 계산됩니다.
따라서 수식에서 2E 로 표기하는 것입니다.
2). Directed

다음으로 방향이 존재하는 그래프에서 Node Degree를 구해보겠습니다.
Undirected와 달리 단순하게 연결된 모든 Edge의 수를 계산하는 것이 아닌 들어오는 Edge에 대한 in-degree와 나가는 Edge에 대한 out-degree를 활용하여 Node Degree를 계산합니다.
노드 C를 기준으로 들어오는 Edge의 수는 2개이기 때문에 in-degree는 2가 되며, 나가는 Edge의 수는 1개이므로 out-degree는 1이고, in-degree와 out-degree를 더한 3이 노드 C의 Node Degree가 됩니다.
또한 모든 노드에 대해 Node Degree의 평균값을 구할 때 Undirected와 다른 점이 있는데 다음의 수식을 통해 확인할 수 있습니다. $ \overline{k}=\frac{E}{N}$
2E 가 아닌 E로 계산하는 이유를 노드 F를 기준으로 설명해 보면 G의 입장에선 나가고, F의 입장에선 들어오기 때문에 in-degree = out-degree가 되어 두 번 계산할 필요가 없는 것입니다.
$$ \overline{k^{in}}=\overline{k^{out}}$$
따라서 2E 가 아닌 E로 계산합니다.
지금은 Node Degree가 어떤 것이고, 어떻게 계산하는지만 알고 넘어가면 될 것 같습니다.
간단하게 설명하자면 Node Degree는 집계(aggregate)하여 업데이트 할 때 정규화(normalization)하는 데 사용됩니다.
추후 GCN 모델에 대해 공부할 때 자세하게 다룰 예정입니다.
이외에도 Node Degree 자체를 하나의 Node Feature로 사용할 수도 있습니다.
즉, 노드의 Feature Vector에 Node Degree 값을 추가하여 GNN의 입력으로 활용하는 것입니다.
이는 노드의 연결성(connectivity)을 모델이 직접 학습할 수 있도록 도와주기도 합니다.
이 정도만 이해하고 구체적인 설명은 추후 진행하겠습니다.

다음으로 그래프를 표현하는 방법으로 인접 행렬(Adjacency Matrix)를 얘기합니다.
왼쪽의 그래프는 Undirected이고, 오른쪽은 Directed 그래프를 표현한 것이며, 아래의 행렬이 각각의 그래프에 해당하는 인접 행렬입니다.
여기서 주목할 점은 Undirected 그래프의 경우 인접 행렬이 대칭적(symmetric)인데, Directed는 인접 행렬이 대칭적이지 못하다(not symmetric)는 차이가 있습니다.

그런데 한가지 더 주의할 점은 인접 행렬로 표현된 실제 그래프 데이터들은 희박하게 존재(sparse)한다는 것입니다.
인접 행렬의 각 원소가 두 노드 사이의 연결 여부를 나타내며 이를 0과 1로 표현하게 되는데 노드의 수는 많은데 연결된 노드의 수가 적으면 해당 그래프 데이터의 인접 행렬은 대부분 0이 되기 때문에 희박하게 존재하게 되는 것입니다.
이런 인접 행렬을 다른 이름으로 희소 행렬(sparse matrix)으로 부르기도 합니다.
희소 행렬은 메모리를 비효율적으로 사용하게 되는 문제가 있는데 GPU가 많이 발전한 지금은 연산에 큰 문제는 되지 않을 것으로 생각합니다.
기존의 해결 방법으로는 연결리스트, CSR 등의 다양한 데이터 구조가 고려되었습니다.

그런데 그래프의 구조는 인접 행렬(Adjacency Matrix)을 변형하여 다양하게 표현할 수 있습니다.
그 중 첫번째로는 연결 강도(weight)를 활용하는 것입니다.
왼쪽의 그래프는 Undirected and Unweighted 그래프로 기존의 Undirected 그래프와 같습니다.
오른쪽의 그래프는 Undirected and Weighted 그래프로 조금 해석해보자면, 2와 4의 경우 연결 강도가 가장 강하고, 이 둘의 연결 강도는 4입니다.
예를 들어보면, 인스타에서 서로의 피드에 좋아요를 많이 누를수록 연결 강도가 강해지는 것입니다.

다음으로 먼저 왼쪽의 그래프는 자기 자신도 고려하는 그래프입니다.
대표적으로 protein(단백질), hyperlink(하이퍼링크)가 있겠습니다.
오른쪽 그래프는 중복된 연결도 포함하는 그래프입니다. 이처럼 다양한 형태의 그래프로 연결 관계를 고려해볼 수 있습니다.
지금까지 CS224W 1주차 내용인 Machine Learning with Graphs 전체를 다뤄봤습니다.
GNN 공부는 처음이라 부족한 부분이 많습니다.
틀린 부분이나 설명이 미흡한 부분은 가감없이 알려주세요!
감사합니다 :D
'정리 필요' 카테고리의 다른 글
| [백준] 1181번 - 단어 정렬 (0) | 2024.11.18 |
|---|---|
| [Python] argparse 사용법 및 예시 (0) | 2024.08.18 |
| [CS224W] Node Degree & Node Centrality (0) | 2024.08.12 |
| LG전자 교육 Time Series 이미지 자료 (0) | 2024.07.29 |
| Github Bio(깃허브 프로필) 줄 바꿈 방법 (0) | 2024.07.29 |



